https://www.acmicpc.net/problem/2042
세그먼트 트리라는 자료구조를 공부해야지..공부해야지 하다가 미뤄놨는데, 삼성 코딩테스트를 준비하면서 공부를 했다. 구현이 복잡해 보였지만, 결국 분할 정복 테크닉을 구간합에서 구현한 것이라는, 생각보다 쉬운 자료 구조였다. 공부할 때는 개발자 영맨님의 유튜브 영상을 참고했다. 현재 나와있는 어느 자료보다 본질적인 부분에 대해서 잘 설명하신 것 같다. 영상을 보고 이 포스트를 보면 되겠다(포스트는 대충 적어놔서 영상 안보고오면 이해가 안 될 것이다..)
https://www.youtube.com/@bluedawnstar
개발자영맨(bluedawnstar)
www.youtube.com
알고리즘 분류
- 세그먼트 트리
- 분할 정복 알고리즘
문제 설명
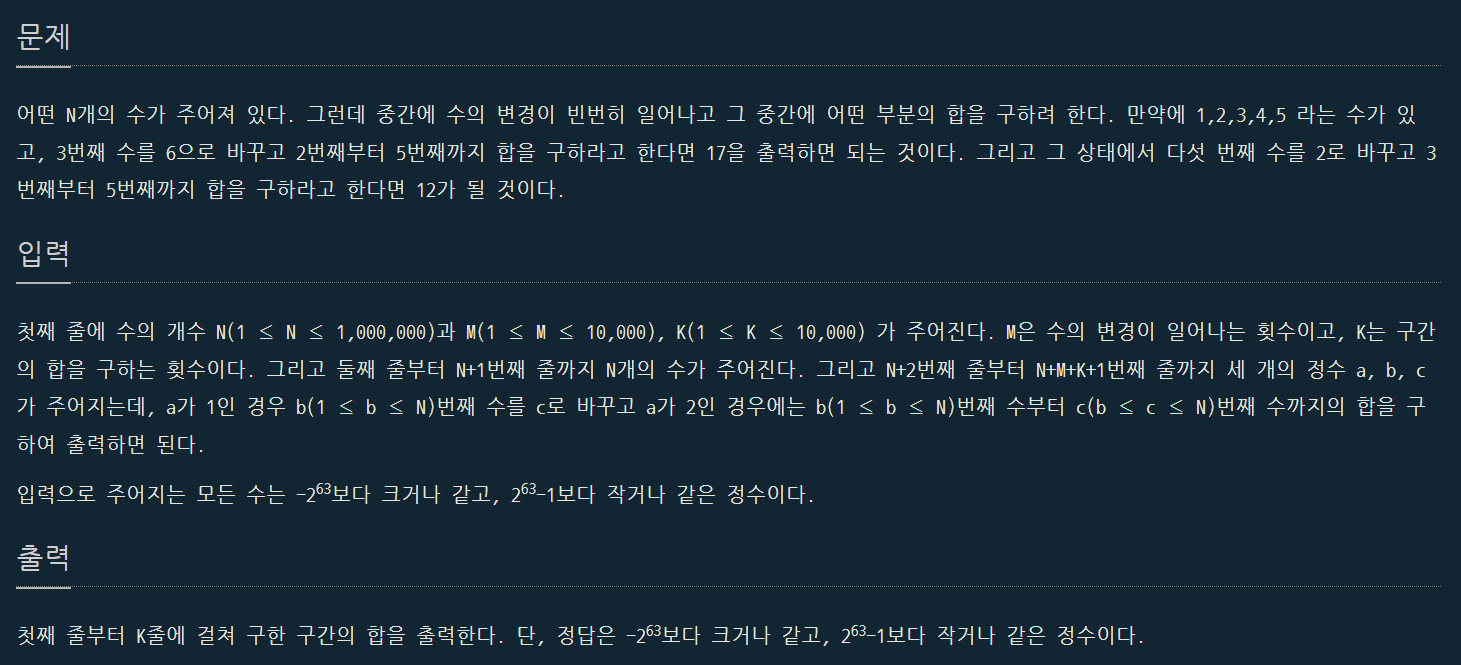
문제 접근
누적합 배열을 구해야 하고, 숫자 범위에 주의해 long long 으로 구현하면 된다.
그런데 문제는, update가 자주 일어나기 때문에 update 한번 하면 O(n)의 시간이 걸린다는 것이다. 따라서 10만개 배열에 만 개의 업데이트가 이루어지므로 10억이다. 따라서 시간 초과가 발생한다.
이를 해결하기 위해서는 업데이트를 O(logN)만에 구할 수 있는 자료구조가 필요하고, 따라서 누적 합을 저장하는 이진 트리를 도입하면 밑이 2인 로그 형태로 업데이트가 가능하며, 각각의 노드에는 범위에 해당하는 누적합을 저장한다.
예를 들어 array a = {1, 3, -2, 8, -7} 이라고 하고 인덱스에 기반한 BST를 구현하면 다음과 같은 누적 합 이진 트리가 구성되며, 이를 세그먼트 트리라고 칭한다.
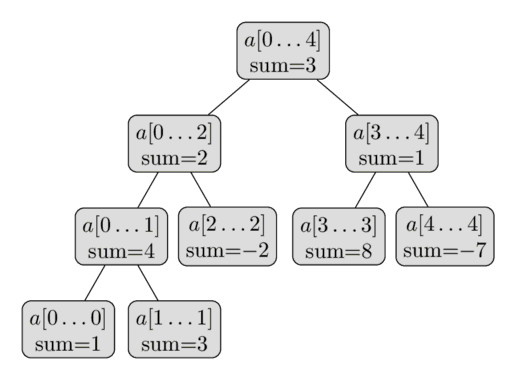
그럼 이진 트리답게, Root 노드의 index = 1로 해야 한다. left = index * 2, right = right * 2 + 1로 접근해야 하기 때문이다.
이후 트리를 구성할 때 leaf 노드는 [누적 left, 누적 right] 값이 같으므로, 배열의 값을 넣어주면 된다. 이 리프 노드를 기반으로 merge하면서 상향식으로 루트 노드 [0 ~ N-1] 의 누적합을 구하면 트리 구성이 완료된다.
int buildRec(const vector<int>& data, int node, int left, int right)
{
if (left == right)
{
return tree[node] = data[left];
}
int mid = (left + right) / 2;
int leftVal = buildRec(data, node * 2, left, mid);
int rightVal = buildRec(data, node * 2 + 1, mid + 1, right);
return tree[node] = merge(leftVal, rightVal);
}Sum을 구하라는 걸 query라고 생각하면, query는 a 부터 b 까지의 누적합이다. 이를 구하기 위해서는 루트 노드부터 계속해서 query를 입력해 [query left ~ query right] 에 해당하는 값만 누적해서 리턴해주면 된다. 만약 쿼리 범위와 노드에서의 범위가 겹치는 부분이 없다면 0을 리턴해주면 된다.
int queryRec(int node, int left, int right, int queryLeft, int queryRight)
{
// 1. 겹치지 않으면 0을 반환한다.
if (right < queryLeft || left > queryRight)
{
return 0;
}
// 2. queryLeft, queryRight 가 left right 범위 안에 있으면 전부 합친다.
if (queryLeft <= left && right <= queryRight)
{
return tree[node];
}
// 3. 일부 겹치면 왼쪽 범위에서 같은 질의값 + 오른쪽 질의값 해서 리턴한다.
int mid = (left + right) / 2;
int leftVal = queryRec(node * 2, left, mid, queryLeft, queryRight);
int rightVal = queryRec(node * 2 + 1, mid + 1, right, queryLeft, queryRight);
return merge(leftVal, rightVal);
}
업데이트를 할 때는 query를 할 때와 거의 같지만, 주목할 것은 어쨌든 root 노드에 update 명령을 던져서 누적해서 상향식으로 업데이트해야 하기 때문에, 만약 범위 안에 updateIndex가 없다면 그대로의 값을 리턴해줘야 한다.
int updateRec(int node, int left, int right, int updateIdx, int newValue)
{
// 1. 겹치지 않으면 업데이트하지않고 현재 자신의 노드를 리턴한다.
// 이렇게 하는 이유는, 아래에서 위로 업데이트할것이므로.
if (updateIdx < left || updateIdx > right)
{
return tree[node];
}
// 2. 딱 그 지점에 도달했다면
if (left == right) // left == right == updateIdx
{
return tree[node] = newValue;
}
// 3. 구간 안에 updateIdx 가 있다면 -> 상향식으로 업데이트할거임(0~N-1)까지
int mid = (left + right) / 2;
int leftVal = updateRec(node * 2, left, mid, updateIdx, newValue);
int rightVal = updateRec(node * 2 + 1, mid + 1, right, updateIdx, newValue);
return tree[node] = merge(leftVal, rightVal);
}이를 통해 세그먼트 트리 구조체를 만들어 주면 문제 다 푼 것이다!!
전체 코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
void fastIO()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
}
typedef struct _SegmentTree
{
ll N;
vector<ll> tree;
ll merge(ll left, ll right)
{
return left + right;
}
_SegmentTree(const vector<ll>& arr)
{
N = arr.size();
tree.resize(N * 4);
buildRec(arr, 1, 0, N - 1);
}
ll buildRec(const vector<ll>& arr, ll node, ll nodeLeft, ll nodeRight)
{
if (nodeLeft == nodeRight)
{
return tree[node] = arr[nodeLeft];
}
ll mid = (nodeLeft + nodeRight) / 2;
ll leftVal = buildRec(arr, node * 2, nodeLeft, mid);
ll rightVal = buildRec(arr, node * 2 + 1, mid + 1, nodeRight);
return tree[node] = merge(leftVal, rightVal);
}
ll queryRec(ll node, ll nodeLeft, ll nodeRight, ll queryLeft, ll queryRight)
{
// 1. query 범위에 nodeleft noderight 없으면 0을 리턴해야함
if (queryRight < nodeLeft || queryLeft > nodeRight)
{
return 0;
}
// 2. query 범위안에 온전하게 nodeleft noderight 있으면 해당 값(누적합) 리턴
if (queryLeft <= nodeLeft && nodeRight <= queryRight)
{
return tree[node];
}
ll mid = (nodeLeft + nodeRight) / 2;
ll leftVal = queryRec(node * 2, nodeLeft, mid, queryLeft, queryRight);
ll rightVal = queryRec(node * 2 + 1, mid + 1, nodeRight, queryLeft, queryRight);
return merge(leftVal, rightVal);
}
ll updateRec(ll node, ll nodeLeft, ll nodeRight, ll updateIdx, ll updateVal)
{
// 1. updateIdx가 범위에 없다면 그대로 리턴(나중에 상향식 누적합 할거니깐)
if (updateIdx < nodeLeft || nodeRight < updateIdx)
{
return tree[node];
}
// 2. left == right == updateIdx
if (nodeLeft == nodeRight)
{
return tree[node] = updateVal;
}
ll mid = (nodeLeft + nodeRight) / 2;
ll leftVal = updateRec(node * 2, nodeLeft, mid, updateIdx, updateVal);
ll rightVal = updateRec(node * 2 + 1, mid + 1, nodeRight, updateIdx, updateVal);
return tree[node] = merge(leftVal, rightVal);
}
ll query(ll left, ll right)
{
return queryRec(1, 0, N - 1, left, right);
}
ll update(ll updateIdx, ll updateVal)
{
return updateRec(1, 0, N - 1, updateIdx, updateVal);
}
}SegmentTree;
int main()
{
fastIO();
int n, m, k;
cin >> n >> m >> k;
vector<ll> data(n);
for (int i = 0; i < n; i++)
{
cin >> data[i];
}
SegmentTree segTree{ data };
for (int i = 0; i < m + k; i++)
{
ll a, b, c;
cin >> a >> b >> c;
if (a == 1)
{
segTree.update(b - 1, c);
}
if (a == 2)
{
cout << segTree.query(b - 1, c - 1) << '\n';
}
}
}이전에는 이 문제를 펜윅 트리로 풀었는데, 확실히 세그먼트 트리로 풀었을 때 메모리 차이가 난다. 하지만, 세그먼트 트리의 장점은 유연성이다! 다이나믹 세그먼트 트리같이 메모리를 아끼기 위한 자료구조는 펜윅 트리로 구성하기 어렵다.

'PS > Baekjoon' 카테고리의 다른 글
| [C++] 23289 : 온풍기 안녕! (0) | 2025.04.02 |
|---|---|
| [C++] 4991 : 로봇 청소기(외판원 순회 풀이) (0) | 2025.03.25 |
| [C++] 11066 : 파일 합치기 (0) | 2025.03.24 |
| [C++] 11049: 행렬 곱셈 순서 (0) | 2025.03.21 |
| [C++] 2749: 피보나치 수 3 (0) | 2025.03.14 |